計算神経科学  ·  2019/07/05

FORCE法によるRecurrent Spiking Neural Networksの教師あり学習

（著）山拓

論文は

Nicola, W. & Clopath, C. Supervised learning in spiking neural networks with FORCE training. Nat. Commun. (2017). (Nat. Commun., arXiv)

 

FORCE(First-Order Reduced and Controlled Error)法は(Sussillo & Abbott, 2009)で提案された学習法で、元々は発火率ベースのRNNに対するオンラインの学習法です。ただし、用いるモデルは一般のRNNとは異なるものです。ユニット間の結合重みはランダムに初期化して固定し、出力の結合重みだけを学習するというタイプのRNNを用います(こういうタイプのNNをReservoir computingと呼びます)。もちろん一般のRNNを学習させるならBack-prop法を用いるのが主流ですが、学習するパラメータが少ないという利点はあります。次に(DePasquale, Churchl & Abbott, 2016)で提案された学習法は、発火率モデルで学習させた後、その活動をSpiking modelに転写するというものです。

 

今回紹介する論文(Nicola & Clopath, 2017)では直接的にFORCE法がSpiking neural networks(SNN)の学習に使用できる、ということです。下図はFORCE法で訓練したSNNの活動の例です。左が学習前、右が学習後です。ここではネットワークからのデコード結果が正弦波となるようにしています(詳細は後述)。

 

この論文(Nicola & Clopath, 2017)を読もうと思ったのは、同一著者の論文(Nicola & Clopath, 2019)でFORCE法が用いられていたためです。(Nicola & Clopath, 2019)は海馬における急速圧縮学習の神経機構をSNNで調べた研究ですが（実はちゃんと理解できていません）、海馬での記憶と再生の機構については(Nicola & Clopath, 2017)でも触れられています。要は計算論的神経科学的に面白いので紹介します。

 

MATLABによる著者実装はModelDBにありますが、今回はPythonで書き直しました。コードはGitHubで公開しています。また、SNNの入門にもなるようにしました。

ニューロンモデル

Spiking ニューロンのモデルとしては

・Theta neuron

・IF (Integrate-and-fire) neuron

・LIF (leaky integrate-and-fire) neuron

・QIF (Quadratic integrate-and-fire) neuron

・Izhikevich neuron

など多くが提案されていますが、今回の記事ではLIF neuronとIzhikevich neuronを扱います。論文では他にTheta neuronも用いられています。

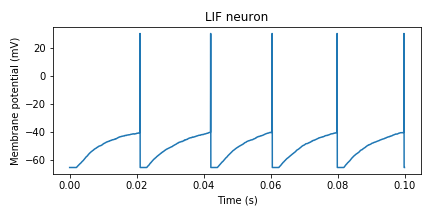
LIF neuron

入力電流を膜電位が閾値に達するまで積分するモデルをIF(integrate-and-fire) neuronといいます。さらに膜電位のleak(漏れ)を考慮したモデルがLIF neuronです。この漏れはイオンの拡散などによるものです。$i$番目のニューロンの膜電位を$v_i$, 入力電流を$I$, 膜電位の時定数を$\tau_m$とすると、式は次のようになります。 $$ \tau_{m} \dot{v}_{i}=-v_{i}+I $$ ここで、$v_i$が閾値$v_{\text{thr}}$を超えると、脱分極が起こり、膜電位は$v_{\text{peak}}$まで上昇します（発火）。発火後、再分極が起こり（過分極は考えません）膜電位は静止膜電位$v_{\text{reset}}$まで低下するとします。さらに発火後の不応期(refractory time period)$\tau_{\text{ref}}$の間は膜電位が変化しない、とします。以上を踏まえて実装すると次のようになります。
# -*- coding: utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm

np.random.seed(seed=0)

dt = 5e-5 # (sec)
T = 0.1 # (sec)
nt = round(T/dt) #Time steps

tref = 2e-3 #Refractory time constant in seconds
tm = 1e-2 #Membrane time constant 
vreset = -65 # Reset voltage(Resting membrane potential) 
vthr = -40 # threshold voltage
vpeak = 30 #

# Initialization
v = vreset #Initialize neuronal voltage with random distribtuions
tlast = 0
v_list = []

# Input
BIAS = -40 # pA
s = np.random.randn(nt)*10 + 5 # pA

# Simulation
for i in tqdm(range(nt)):
    # Update
    I = s[i] + BIAS
    dv = ((dt*i) > (tlast + tref))*(-v + I) / tm #Voltage equation with refractory period 
    v = v + dt*dv
    
    # Check firing    
    tlast = tlast + (dt*i - tlast)*(v>=vthr) #Used to set the refractory period of LIF neurons 
    v = v + (vpeak - v)*(v>=vthr) 
    
    # Save
    v_list.append(v) 
    
    # Reset
    v = v + (vreset - v)*(v>=vthr) #reset with spike time interpolant implemented.
    
# Plot
t = np.arange(nt)*dt
plt.figure(figsize=(6, 3))
plt.plot(t, np.array(v_list))
plt.title('LIF neuron')
plt.xlabel('Time (s)')
plt.ylabel('Membrane potential (mV)') 
plt.tight_layout()
plt.savefig('LIF_neuron.png')
#plt.show()

次にforループ内の重要な部分の解説をします。 

dv = ((dt*i) > (tlast + tref))*(-v + I) / tm #Voltage equation with refractory period
この部分ですが、tlastが最後にスパイクの生じた時間を記録する変数、trefが不応期の時間となっています。dt*iで現在のシミュレーション時間が計算されるので、 dt*iがtlast+trefを超えないと膜電位変化dvは0となります。不等式によるステップ関数を上手く使うのがポイントです。こうすることでif文を用いずに実装することができます。

次にスパイクが生じるかの確認です。 
tlast = tlast + (dt*i - tlast)*(v>=vthr) #Used to set the refractory period of LIF neurons
v = v + (vpeak - v)*(v>=vthr)
36行目はtlastの更新式です。ここでも不等式を上手く使っています。(v>=vthr)がTrueならtlast = dt*iとなり、Falseならtlastは変わりません。37行目はなくても良いですが、発火したときの膜電位変化を表現したい場合にはいれると良いです（結局43行目のようにresetします）。

Izhikevich neuron

(Izhikevich, 2003)で考案されたモデルです。簡素な微分方程式ですが、様々なニューロンの活動を模倣することができます。 \begin{align*} C\dot{v}_{i}&=k\left(v_{i}-v_r\right)\left(v_{i}-v_t\right)-u_{i}+I \\ \dot{u}_{i}&=a\left(b\left(v_{i}-v_{r}\right)-u_{i}\right) \end{align*} ここで、$C$は膜容量(membrane capacitance), $v_r$は静止膜電位,$v_t$は閾値電位, $a$はadaptation time constantの逆数, $k$は活動電位の半値幅の制御に関わるパラメータ, $b$は$u$の$v$に対する感受性(共鳴度合い)です。閾値は$v_t$ですが、シミュレーション上での膜電位のリセットは$v$が$v_{\text{peak}}$を超えた時です(これはLIF neuronと異なる点です)。このとき、 \begin{align*} u&\leftarrow u+d\\ v&\leftarrow v_{\text{reset}} \end{align*} とします。ただし、$v_{\text{reset}}$は過分極を考慮して静止膜電位$v_r$よりも小さい値とします。以上を踏まえて、シミュレーションの例と実装は次のようになります。
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm

np.random.seed(seed=0)

T = 1000 #Total time in ms
dt = 0.04 #Integration time step in ms 

nt = round(T/dt) #Time steps

C = 250 #capacitance
vr = -60 #resting membrane 
b = -2 #resonance parameter 
ff = 2.5 #k parameter for Izhikevich, gain on v 
vpeak = 30 # peak voltage
vreset = -65 # reset voltage 
vt = vr + 40 - (b/ff) #threshold  
a = 0.01 #adaptation reciprocal time constant 
d = 200 #adaptation jump current 

# Initialization
v = vr #Initialize neuronal voltage with random distribtuions
v_ = v #These are just used for Euler integration, previous time step storage
u = 0
v_list = []
u_list = []

# Input
BIAS = 1000 # pA
s = np.random.randn(nt)*300 + 100 # pA

# Simulation
for i in tqdm(range(nt)):
    # Update
    I = s[i] + BIAS
    v = v + dt*((ff*(v - vr)*(v - vt) - u + I)) / C  # v(t) = v(t-1)+dt*v'(t-1)
    u = u + dt*(a*(b*(v_-vr)-u)) #same with u, the v_ term makes it so that the integration of u uses v(t-1), instead of the updated v(t)
    
    # Reset
    u = u + d*(v>=vpeak) #implements set u to u+d if v>vpeak, component by component. 
    v = v + (vreset-v)*(v>=vpeak) #implements v = c if v>vpeak add 0 if false, add c-v if true, v+c-v = c
    v_ = v # sets v(t-1) = v for the next itteration of loop
    
    # Save
    v_list.append(v) 
    u_list.append(u) 
    
# Plot
t = np.arange(nt)*dt*1e-3
plt.figure(figsize=(6, 5))
plt.subplot(2,1,1)
plt.title('Izhikevich neuron')
plt.plot(t, np.array(v_list))
#plt.xlabel('Time (s)')
plt.ylabel('Membrane potential (mV)') 
 
plt.subplot(2,1,2)
plt.plot(t, np.array(u_list))
plt.xlabel('Time (s)')
plt.ylabel('u(t)') 

plt.tight_layout()
plt.savefig('Izhikevich_neuron.png')
#plt.show()

シナプスモデル

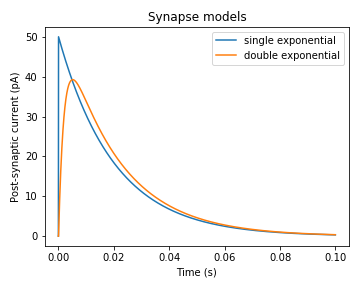
スパイクが生じたことによる膜電位変化は軸索を伝播し、シナプスによって次のニューロンへと発火が伝わります。このとき、神経伝達物質の放出、シナプス後膜の受容体への神経伝達物質の結合、イオンチャネル開口によるシナプス後電流(postsynaptic current; PSC)の発生、という過程が起こります（ざっくりとした説明ですが）。そのため、スパイク列(spike train)は次のニューロンにそのまま伝わるのではなく、ある種の時間的フィルターをかけられて伝わります（このフィルターをsynaptic filterと呼びます）。Synaptic filter(またはsynapse model)としてはsingle exponential synaptic filterやdouble exponential synaptic filterがあります。シナプス前ニューロンにおいてスパイクが生じてからのPSCの変化はおおよそ指数関数的に減少する、というのがsingle exponential synaptic filterで、2重の指数関数によりPSCの立ち上がりも考慮するのが、double exponential synaptic filterです。数式の前に挙動を示します。以下の図は2種類のモデルにおいてt=0でスパイクが生じてからのPSCの変化を示しています。 

import numpy as np
import matplotlib.pyplot as plt
import math

dt = 5e-5 # (sec)
td = 2e-2 #synaptic decay time
tr = 2e-3 #synaptic rise time
T = 0.1 # (sec)
nt = round(T/dt) #Time steps

# synapse for single exponential 
r = 0 # initial
single_r = [] 
for i in range(nt):    
    if i == 0:
        spike = 1
    else:
        spike = 0
    single_r.append(r)
    r = r*math.exp(-dt/td) + spike/td
    #r = r*(1-dt/td) + spike/td

# synapse for double exponential
r = 0; hr = 0; # initial
double_r = []
for i in range(nt):    
    if i == 0:
        spike = 1
    else:
        spike = 0
    double_r.append(r)
    r = r*math.exp(-dt/tr) + hr*dt 
    hr = hr*math.exp(-dt/td) + spike/(tr*td)
    #r = r*(1-dt/tr) + hr*dt 
    #hr = hr*(1-dt/td) + spike/(tr*td)

# Plot
t = np.arange(nt)*dt
plt.figure(figsize=(5, 4))
plt.plot(t, np.array(single_r), label="single exponential")
plt.plot(t, np.array(double_r), label="double exponential")
plt.title('Synaptic models')
plt.xlabel('Time (s)')
plt.ylabel('Post-synaptic current (pA)') 
plt.legend()
plt.tight_layout()
plt.savefig('Synapse.png')
#plt.show()

 

ただし、実際のPSCはこれに結合重みを乗じて総和を取ったものとなります。結合重みというのは計算する上での仮想的なもので、実際には神経伝達物質の種類や、その受容体の数など複数の要因によって決定されています。

 

Single exponential synaptic filter

単にスパイクが起こってから指数関数的にその影響（神経伝達物質の放出など）が減少する、というモデルです。式は次のようになります。 $$ \dot{r}_{j}=-\frac{r_{j}}{\tau_{s}}+\frac{1}{\tau_{s}} \sum_{t_{j k}<t} \delta\left(t-t_{j k}\right) $$ ここで${r}_{j}$が$j$番目のニューロンの出力(これに結合重みをかけて総和を取ることでPSCとなるので、こういう表現をしています)、$\tau_s$がシナプスの時定数(synaptic time-constant)、$t_{j k}$は$j$番目のニューロンの$k$番目のスパイクです。また、$\delta(\cdot)$はDiracのdelta関数です（ただし$\delta(0)=1$です）。これをEuler法で差分化すると $$ r_j(t+\Delta t)=\left(1-\frac{\Delta t}{\tau_{s}}\right)r_j(t)+\frac{1}{\tau_{s}} \delta_{t,t_{j k}} $$ となります。ここで$\delta_{t,t_{j k}}$はKroneckerのdelta関数で、$t=t_{j k}$のときに1, それ以外は0となります。ただし、著者実装では $$ r_j(t+\Delta t)=\exp\left(-\frac{\Delta t}{\tau_{s}}\right)r_j(t)+\frac{1}{\tau_{s}} \delta_{t,t_{j k}} $$ となっています。数値的にはほぼ同じですがなぜでしょう…。

Double exponential synaptic filter

次はスパイクが生じて、しばらくしてから神経伝達物質の放出がピークとなるようなモデルです。式は次のようになります。 \begin{align*} \dot{r}_{j}&=-\frac{r_{j}}{\tau_{d}}+h_{j}\\ \dot{h}_{j}&=-\frac{h_{j}}{\tau_{r}}+\frac{1}{\tau_{r} \tau_{d}} \sum_{t_{j k}<t} \delta\left(t-t_{j k}\right) \end{align*} ここで$\tau_{r}$をsynaptic rise time, $\tau_{d}$をsynaptic decay timeと言います。$\tau_{d}$は$\tau_{s}$と同じく神経伝達物質の減少速度を決定しています。また、$\tau_{r}=\tau_{d}$の場合はAlpha synapseと呼ぶこともあります。次に、同じようにEuler法で差分化すると \begin{align*} r_j(t+\Delta t)&=\left(1-\frac{\Delta t}{\tau_{d}}\right)r_j(t)+h_j(t)\cdot \Delta t\\ h_j(t+\Delta t)&=\left(1-\frac{\Delta t}{\tau_{r}}\right)h_j(t)+\frac{1}{\tau_{r}\tau_{d}} \delta_{t,t_{j k}} \end{align*} となります。これまた著者実装は \begin{align*} r_j(t+\Delta t)&=\exp\left(-\frac{\Delta t}{\tau_{d}}\right)r_j(t)+h_j(t)\cdot \Delta t\\ h_j(t+\Delta t)&=\exp\left(-\frac{\Delta t}{\tau_{r}}\right)h_j(t)+\frac{1}{\tau_{r}\tau_{d}} \delta_{t,t_{j k}} \end{align*} となっています。

ネットワークの入出力

再帰的な入力

ここからが論文の内容です。今回のネットワークには特別な入力があるわけではなく、再帰的な入力によって活動が持続しています。$i$番目のニューロンの入力は$I_i=s_i+I_{\text{Bias}}$ですが、この$s_i$は $$ s_{i}=\sum_{j=1}^{N} \omega_{i j} r_{j} $$ として計算されます。$r_j$が$j$番目のニューロンの出力(シナプスフィルターをかけられたスパイク列), $\omega_{i j}$は$j$番目のニューロンから$i$番目のニューロンへの結合重みを意味します。

次にニューロンの活動$r_j$を線形にデコードし、その結果を教師信号に近づけます。教師信号を$\boldsymbol{x}(t)$とし、デコードした出力を $$ \hat{\boldsymbol{x}}(t)=\sum_{j=1}^{N} \phi_{j} r_{j} $$ とします。$\phi_j$は$j$番目のニューロンの出力における結合重みです。

ここから少しややこしいのですが、ネットワークの重み$\Omega=[\omega_{ij}]$は $$ \omega_{i j}=G \omega_{i j}^{0}+Q \eta_{i} \cdot \phi_{j}^{T} $$ となっています。$\omega_{i j}^{0}$は固定された重みです。$G, Q$は定数で、$\eta_{i}$は-1か1にランダムに決まられた値です。よって学習するパラメータは$\phi_{j}$のみです。

ここでバイアスを抜いた入力電流$s_{i}$は次のように分割できます。 \begin{align*} s_{i}&=\sum_{j=1}^{N} \omega_{i j} r_{j}\\ &=\sum_{j=1}^{N} \left(G \omega_{i j}^{0}+Q \eta_{i} \cdot \phi_{j}^{T}\right)r_{j}\\ &=Q \boldsymbol{\eta} \hat{\boldsymbol{x}}(t)+\sum_{j=1}^{N} G \omega_{i j}^{0}r_{j} \end{align*} これは実装する際に必要となります。

固定結合重みの初期化

固定された結合重み$\omega_{i j}^{0}$は$\mathcal{N}(0, (Np)^{-1})$の正規分布からランダムサンプリングした値です($N$はニューロンの数、$p$は定数)。ただし、各ニューロンが投射される重みの平均が0になるようにスケーリングします。

FORCE法とRLSによる結合重みの更新

FORCE法ではRLS(Recursive Least Squares)学習という手法を用います(ネットワークの構造も含めてFORCE法というべきか同義なのかは分かりません)。

誤差を $$ \boldsymbol{e}(t)=\hat{\boldsymbol{x}}(t)-\boldsymbol{x}(t) $$ とした場合、出力重み$\phi$を次の式で更新します。 \begin{align*} \phi(t)&=\phi(t-\Delta t)-e(t) \boldsymbol{P}(t) \boldsymbol{r}(t)\\ \boldsymbol{P}(t)&=\boldsymbol{P}(t-\Delta t)-\frac{\boldsymbol{P}(t-\Delta t) \boldsymbol{r}(t) \boldsymbol{r}(t)^{T} \boldsymbol{P}(t-\Delta t)}{1+\boldsymbol{r}(t)^{T} \boldsymbol{P}(t-\Delta t) \boldsymbol{r}(t)} \end{align*} ここで$\boldsymbol{P}(t)$はニューロンの相関行列の逆行列という設定です。 $$ \boldsymbol{P}(t)^{-1}=\int_{0}^{t} \boldsymbol{r}(t) \boldsymbol{r}(t)^{T} \mathrm{d} t+\lambda I_{N} $$ また、この手法で更新することは次の損失関数$C$を最小化することとなります。 $$ C=\int_{0}^{T}(\hat{\boldsymbol{x}}(t)-\boldsymbol{x}(t))^{2} \mathrm{d} t+\lambda \phi^{T} \phi $$ ここで初期値は$\phi(0)=0, \boldsymbol{P}(0)=I_{N}\lambda^{-1}$です。$I_{N}$は$N$次の単位行列を意味します。$\lambda$は正則化のための定数です。

正弦波(sine wave)の学習

それではFORCE法を用いてSNNを訓練してみましょう。教師信号は正弦波とします。これは論文中のFig.2Cに対応します。以下はFORCE法のコアの部分です。 

# Implement RLMS with the FORCE method 
z = BPhi.T @ r #approximant 
err = z - zx[i] #error 

# RLMS 
if i % step == 1:
    if i > imin:
        if i < icrit:
            cd = (Pinv @ r)
            BPhi = BPhi - (cd @ err.T)
            Pinv = Pinv - (cd @ cd.T) / (1.0 + r.T @ cd)

誤差errを計算し、計算ステップがiminを超えた後、stepごとに$\phi$(BPhi)と$\boldsymbol{P}(t)$(Pinv)を更新します。

実装におけるその他の部分はニューロンモデルとシナプスモデルで紹介した実装を参考にすると理解しやすいと思います。

LIF neuronの場合

LIF neuronを用いたFORCE法の実装はLIF_FORCE_sinewave.pyです。この記事の冒頭にも貼りましたが、下図はネットワークの活動を示しています。左側が学習前(0s~1s)、右側が学習後(14s~15s)です。

 

次に、12s~15sにおけるデコードされた出力(青)と教師信号(オレンジ)です。少しずれていますが、これは仕様です（Supplement materialでもずれていたので…）。

最後に、見てもあまり分からないのですが、重みの固有値の変化です。

Izhikevich neuronの場合

Izhikevich neuronを用いたFORCE法の実装はIzhikevich_FORCE_sinewave.pyです。LIF neuronの場合と同様に下図はネットワークの活動で、左側が学習前(0s~1s)、右側が学習後(14s~15s)です。

 

次に、12s~15sにおけるデコードされた出力(青)と教師信号(オレンジ)です。Izhikevich neuronの方がLIF neuronよりも結果が綺麗な気がします。

重みの固有値は省略します(見てもやっぱりよくわからないので)。

 

鳥の鳴き声の再現と海馬の記憶と再生

詳しくは説明しませんが、論文中では教師信号として正弦波以外にもVan der Pol方程式やLorenz方程式の軌道を用いて実験しています。さらに教師信号としてベートーヴェンの歓喜の歌(Ode to joy)や鳥の鳴き声を用いても学習可能であったようです。

 

話は少しずれますが、小鳥の運動前野であるHVCには連鎖的に結合したニューロン群が存在します。これはリズムを生み出すための計時に関わっているといわれています(この話は、D. Buonomano(著), 村上郁也 (翻訳)『脳と時間』(amazon)に書いてありますので気になる方はお読みください(ダイレクトマーケティング))。

 

カナリアのHVCニューロンを実験的に損傷(ablation)させると歌が歌えなくなるという実験がありますが、同様にSNNのHVCパターンをablationすると学習した歌が再生できなくなったようです。このような計時に関わるパターンをHDTS(high-dimentional temporal signal)と著者らは呼んでいます。HDTSを学習させた後に歓喜の歌を学習させると、HDTSがない場合よりも短い時間かつ高精度で学習できたようです。

 

さらにHDTSを外部入力とし、同時に映像を学習させる、という実験もしています(HDTSを内的に学習させる場合も行っています)。ネットワークは記録した映像を実時間で再生することができましたが、外部信号のHDTSを加速させることで圧縮再生が可能だったそうです。さらにHDTSを逆にすると、逆再生もできたそうです。

 

ニューロンの発火のタスク依存的な圧縮は実験的に観察されています(例えばEuston, et al., 2007)。空間的な課題(箱の中に入れて探索させるなど)をラットにさせると、課題中に記憶された場所細胞の順序だった活動は、ラットの睡眠中に圧縮再生されるという実験結果があります。その圧縮比は5.4〜8.1だったそうですが、この比率はSNNが映像を大きな損失なく再生できる圧縮比とほぼ同じであったようです(面白い)。

 

というわけでSNNはFORCE法で訓練できる、というこの論文はHDTSの重要性を示しているものでもあったということです。この辺が研究者としてのレベルの違いを感じます(辛い)。

 

まとめ

ということでSNNの入門とFORCE法による訓練について解説しました。自分はRNNを用いた計算論的神経科学について主に研究してきましたが(論文は未だに出せてないですががが)、最近の発火率モデルのRNNの研究でも「spiking neuronを用いて更なるbiological plausibleな研究を次にしたいぜ」的なことを書いている論文がちらほらみられるので、発火率モデルからspiking モデルへの過渡期なのかもしれません。

 

参考文献

・Sussillo, D. & Abbott, L. F. Generating coherent patterns of activity from chaotic neural networks. Neuron. 63, 544–557 (2009). (pdf)

・DePasquale, B., Churchland, M. M. & Abbott, L. Using firing-rate dynamics to train recurrent networks of spiking model neurons. Preprint at https://arxiv.org/abs/1601.07620 (2016).

・Nicola, W. & Clopath, C. A diversity of interneurons and Hebbian plasticity facilitate rapid compressible learning in the hippocampus. Nat. Neurosci. 22, 1168–1181 (2019)

・Izhikevich, E.M. Simple model of spiking neurons. IEEE. 2003

・Roth,A. & Rossum, M. Modeling Synapses. 2009. (pdf)

・Euston, D. R., Tatsuno, M. & McNaughton, B. L. Fast-forward playback of recent memory sequences in prefrontal cortex during sleep. Science 318, 1147–1150 (2007).

 

・Notes on “Supervised learning in spiking neural networks with FORCE training”

・https://neuronaldynamics.epfl.ch/index.html

 

Reservoir computingについて

Reservoir computingについてはもう少し丁寧に書いた方が良いかと思いましたが、既に色々記事があるので省略しました。

・ちょっと変わったニューラルネットワーク Reservoir Computing

・Reservoir Computingとは

・Reservoir computing - Wikipedia

 

コメントをお書きください

コメント: 2
  • #1

    take (土曜日, 21 9月 2019 16:54)

    ifを使わない書き方には恐れ入りました

  • #2

    無名 (火曜日, 12 1月 2021 20:27)

    元論文の式(2)に示されている
    r_j=F√s_j(s_j>=0), 0(s_j<0)
    はプログラムのどの部分にあたるのでしょうか？